Classical Test Theory and Item Response Theory
 INTRODUCTORY
INTRODUCTORY
“You should look at this section if you have only a limited understanding of CTT and IRT.”
Perhaps the most technically complicated part of an assessment programme is the use of psychometric analysis. While this is not required for small scale assessments at the classroom and school level, it is widely used in large scale assessment.
The term ‘psychometrics’ refers to scientific ways of measuring a particular ability. This could be the ability to manage time or the ability to write well. Psychometrics allows for conclusions to be drawn from test scores to report on student ability. For example, the results of a reading assessment can provide information on the reading ability of pupils in a specific classroom or school, and how they compare with other pupils in the same, as well as in different, classrooms and schools.
The most common approaches used by psychometrics are classical test theory (CTT) and item response theory (IRT), and both can be used to build a good measuring instrument. CTT is often use due to its relative simplicity, and the lower level of skill required to undertake analysis. But is has a number of limitations.
Most importantly, CTT can only be used to analyse the performance of one group of students on one assessment instrument. If a different group of students takes that assessment instrument, or if the same group of students takes another assessment instrument, then comparisons cannot be made.
CTT assumes that all items in an assessment instrument make an equal contribution to the performance of students. IRT, in contrast, takes into account the fact that some items are more difficult than others. This means that the probability of success on items is due both to student ability and also to item difficulty.
Second, the use of IRT allows descriptions to be developed that explain exactly what students at each level of performance know and can do. For example, they might explain that a Level 1 student can only calculate the circumference of a rectangle, while a Level 2 student can also calculate the circumference of a circle. This detailed level of reporting is very helpful in explaining performance to education stakeholders, and also in identifying the next level that students need to reach. It can also be used in setting benchmarks.
Third, IRT analysis of individual items can identify which items have the correct level of difficulty for a cohort of students and which items are able to distinguish between students with different levels of ability. Items that don’t achieve these standards (for example when the data from a pilot study is analysed) can then be either revised or removed, ensuring that the overall assessment instrument is a better measure of student achievement.
Key concepts in both CTT and IRT theories are reliability and validity. A reliable measure is one that measures a construct consistently across time, individuals, and situations. This means that if it was repeated multiple times it would be likely to produce the same results each time.
A valid measure is one that measures what it is intended to measure. For example, a mathematics test that give students mathematics problems to solve is likely to be a valid measure of mathematics. But a mathematics test that requires students to read complex texts about mathematics is likely to be measuring reading ability, not mathematics ability.
Overall, IRT is a more sophisticated model than CTT and has become dominant in assessment programmes, including those conducted at the national, regional and international levels. Undertaking IRT does, however, require a much higher level of technical skill to undertake than CTT and this skill needs to be developed through higher level educational studies and practice over a long period of time.
To find out more about CTT and IRT, move to #Intermediate.
 INTERMEDIATE
INTERMEDIATE
” You should look at this section if you already know something about CTT and IRT and would like to know more details. “

The term ‘psychometrics’ refers to scientific ways of measuring a particular ability. This could be the ability to manage time or the ability to write well. The ability is a latent trait which means it cannot be directly observed. For example, it is not possible to look into the brains of students and identify their mathematical processing skills. This is very different to the way that physical attributes (e.g. height or temperature) can be observed. Therefore, psychometrics is about measuring latent traits through collecting information associated with them, through tests and assessments.
The greatest value for an assessment programme is achieved if pupil’s performance is reported using scale scores. Scaling involves developing a common unit of measurement and then converting student performance to scale scores and showing them on the scale. There is more than one approach to scaling and the choice between them should relate to the purpose of the assessment programme. Common approaches are Classical Test Theory (CTT) and Item Response Theory (IRT).
For a long time CTT was the dominant psychometric theory. CTT focuses on reliability and assumes that a test score includes both the true score (that a candidate could obtain in a perfect situation) and error. The error represents the fact that no assessment instrument is perfect.
CTT is still used today, partly due to its relative simplicity, and the lower level of skill required to undertake analysis. But is has a number of limitations. Most importantly, CTT can only be used to analyse the performance of one group of students on one assessment instrument. If a different group of students takes that assessment instrument, or if the same group of students takes another assessment instrument, then comparisons cannot be made.
The main limitation of CTT is that it does not allow students’ scores to be compared over time unless the identical assessment instrument is used. Moreover, CTT also only allows for student ability to be described between 0% and 100% correct on a test. It is not possible to make generalisations about the underlying ability (e.g. reading skills) that pupil may possess.
In contrast, under the approaches of IRT, there is an explicit latent trait defined in the model, and assessment instruments measure the level of the latent trait in each individual.
IRT refers to a family of mathematical models that attempt to explain the relationship between latent traits (e.g. reading ability) and their manifestations (i.e. pupil’s performance on a reading test).
IRT establishes a link between assessment items (questions in the test), students responding to these items and the underlying trait being measured (reading ability). The main principle is that the ability and items can be located on the same unobservable continuum, and the main purpose focuses on establishing the student’s position on that continuum. The image below shows how student abilities (on the left) and item difficulties (on the right) can be separated but shown on the same scale.
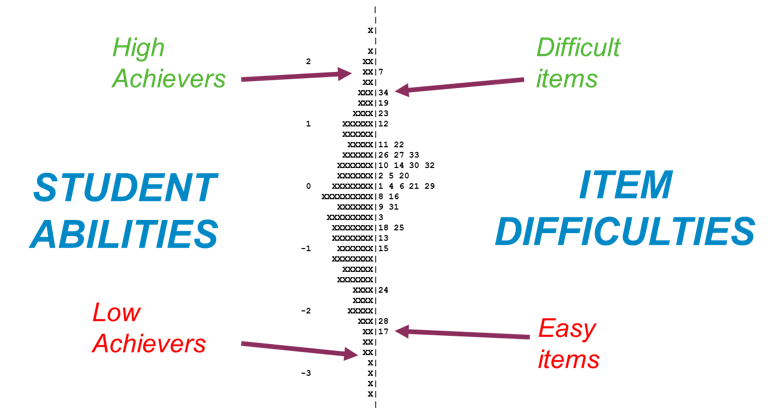
IRT is considered more advantageous than CTT (and is widely used internationally) as it focuses on describing student ability against the underlying skill. This could be reading ability or writing ability. It also enables the comparison of students at different grade levels and for the performance of students to be compared over time.
These benefits make IRT very valuable for large scale assessments which are designed to provide evidence to help educational policy-makers and practitioners improve the quality of education. IRT is, however, more advanced and requires a higher level of technical skill to undertake than CTT. IRT focuses on estimating the probability of a student responding correctly to an item.
IRT can be used throughout the process of:
- adapting the measurement instrument tool to different settings
- field testing the assessments
- training developers to standardise the data collection
- sampling schools
- administering tools to the sample of students
- analysing the data
- generalising the baseline results to the target population.
Whatever the approach used to the analysis of assessment data, it should be carefully aligned with the purpose of the assessment. The choice should also take into account the availability of skilled staff. Scaling requires a high level of technical expertise and this is often not available at the district, state or even national level.
To find out more about IRT, move to #Advanced.
 ADVANCED
ADVANCED
” You should look at this section if you are already familiar CTT and IRT. “
One of the most common forms of IRT is the Rasch Model which links student ability (the latent trait) to the difficulty of each item and is known as the one-parameter logistic model. There are other models but the Rasch model has the strongest construct validity (the extent to which a test measures what it says it measures) and is best suited to measurement over time. This is why it is used in large international assessment programmes such as PISA, TIMSS and PIRLS, as well as in many high quality national and regional assessment programmes.
The Rasch model uses estimates of the person’s ability (β) and task difficulty (δ) to model a probability (P) of success of that person succeeding on a task based on the mathematical relationship of these three factors. β and δ are the model’s parameters that are estimated through the analyses of the observations – they are estimates only since we cannot know the true ability.
The main principle is that the difference between β and δ is related to the P (the higher the difference, the higher the probability of success). Both β and δ are locations on the on the same continuous variable. They are represented through logits. The logit scale has an arbitrary origin, and the location of the estimates can be shifted without it affecting the relative difference between these parameters.
The estimates of β are produced by analysing the counts of success or failure of an individual on a specific number of tasks. The estimates of δ are produced by analysing the number of individuals who succeed or fail on the task. To ensure reliability, estimates are based on a number of observations. Moreover, the conditions of observations need to be standardised.
When we have estimates of person and item parameters, it is possible to map them onto the same scale since both estimates are expressed in logits – this is usually referred to as a Wright Map. The scale is placed in the middle, with the assessment items locates on the right and students on the left. This illustrates the ranking of students and items – which items have a higher or lower chance of being answered correctly and which items are most suitable for the ability level of which students. It is also possible to include details for students (e.g. demographic characteristics) and items (e.g. learning sub-domains).
Constructing a Wright Map provides benefits to testing process, since it provides a clear overview of where learners are located based on their skills and knowledge. Another advantage of mapping the item and persons estimates on the same map is that it illustrates a learning progression.
These ‘proficiency scales’ provide an evidence based illustration of how knowledge and skills are developed within a certain area. By understanding the relationship between persons and items, we can understand how learning in that domain builds up: which are the steps that one needs to master before advancing to a higher level of understanding.
About the guidance levels
